Send
Close Add comments:
(status displays here)
Got it! This site "robinsnyder.com" uses cookies. You consent to this by clicking on "Got it!" or by continuing to use this website. Note: This appears on each machine/browser from which this site is accessed.
Longest common subsequence
1. Longest common subsequence
These notes were originally presented at the 2012 Lua Conference as Incrementally developing and implementing Hirschberg's longest common subsequence algorithm using Lua.
They have been revised, updated, and changed for this page.
2. Longest common subsequence
|
nematode-knowledge
empty-bottle
 emt-ole
|
The
LCS = Longest Common Subsequence problem is a dual problem of the
SED = Shortest Edit Distance problem.
The solution to these problems are used in open source file comparison tools such as WinMerge and DiffMerge.
In 1974, Hirschberg published a reasonably space and time efficient solution to these problems.
3. Subsequence
Technical definition of a subsequence.
String C = c
1c
2...c
p is a
subsequence of string A = a
1a
2...a
m if there as a mapping
F: [1, 2, ..., p] to [1, 2, ..., m]
such that F(i) = k only if c
i is a
k and F is a monotone strictly increasing function (that is, (F(i) = u) and (F(j) = v) and (i < j) imply that (u < v)).
4. Common subsequence
String C is a
common subsequence of strings A and B iff
C is a subsequence of A and
C is a subsequence of B.
5. Problem
Given strings
A = a
1a
2...a
m and
B = b
1b
2...b
n
find string
C = c
1c
2...c
p
such that C is a common subsequence of both A and B and p is maximized. C is then called a
maximal common subsequence or
Longest Common Subsequence.
6. Alphabet
Alphabets examples:
Characters (line comparison)
Lines (file comparison)
Nucleotides (DNA comparisons)
7. Example strings

Example strings:
a = "nematode-knowledge"
m = 18
b = "empty-bottle"
n = = 12
8. LCS
 No connection lines cross.
In general there are more than one LCS (e.g., last "e").
No connection lines cross.
In general there are more than one LCS (e.g., last "e").
9. Symbols
Symbols can be anything that can be matched.
Letters of an alphabet
Lines of text
Nucleotides (in DNA)
For example purposes, letters will be used.
10. DNA
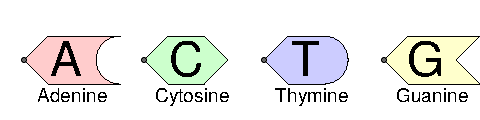
DNA consists of a sequence of four different nucleotides.
Adenine
Cytosine
Thymine
Guanine
11. DNA
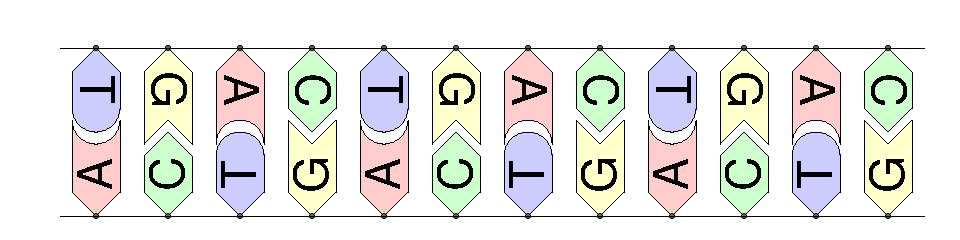
AGGCTATCACCTGACCTCCAGGCCGATGCCC...
TAGCTATCACGACCGCGGTCGATTTGCCCGAC...
The DNA sequence is about 3 billion nucleotides (6 billion bits) for a human.
12. DNA code
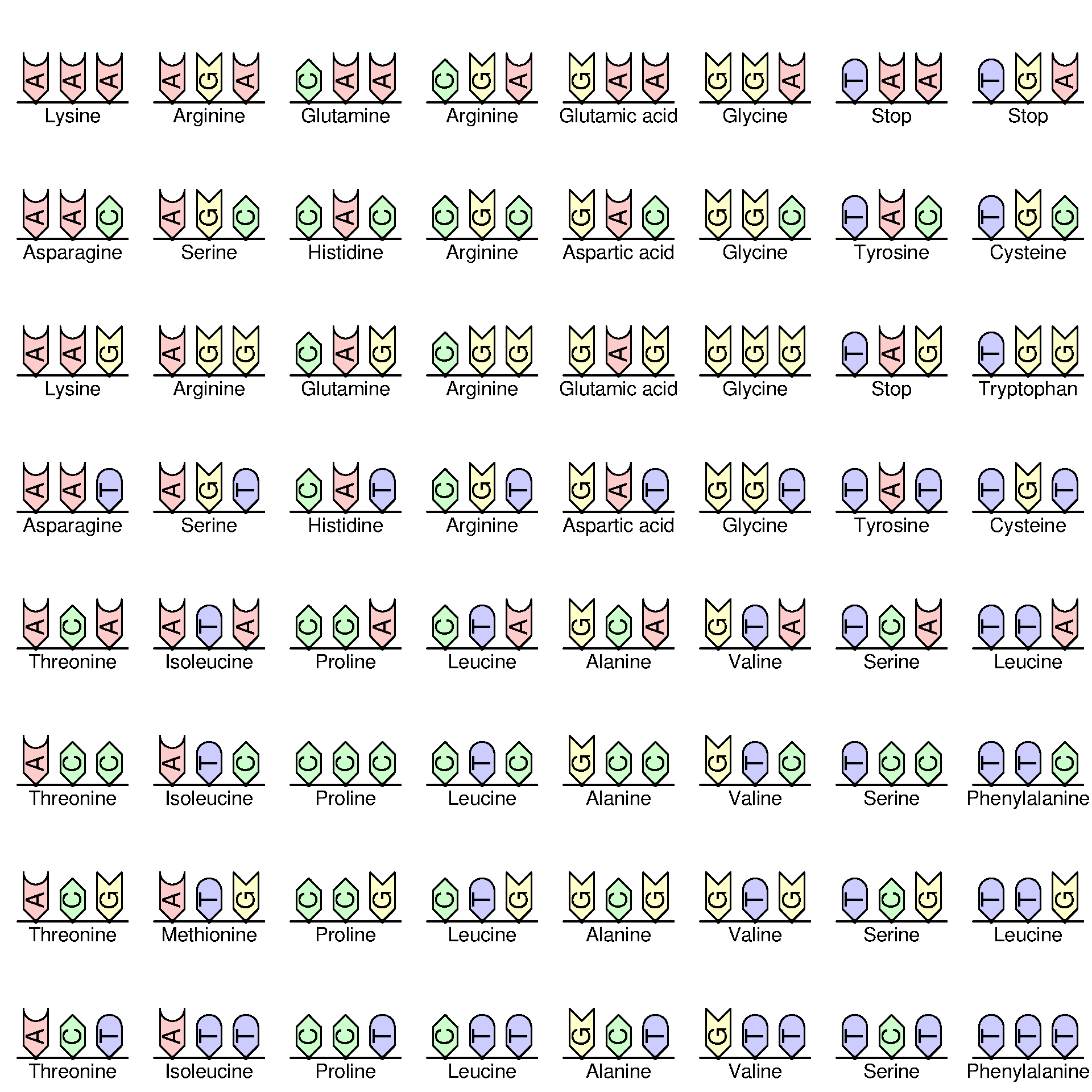
Three nucleotides go together to specify one amino acid (or start or stop instructions).
The 4*4*4 = 64 triples specify 64 codes.
13. WinMerge

File comparison: (line oriented, useful for regression testing, etc.):
WinMerge at http://www.winmerge.org.
Useful WinMerge setting:
Select "Edit", "Options...".
Uncheck "Close windows with ESC".
14. DiffMerge
15. Line comparison
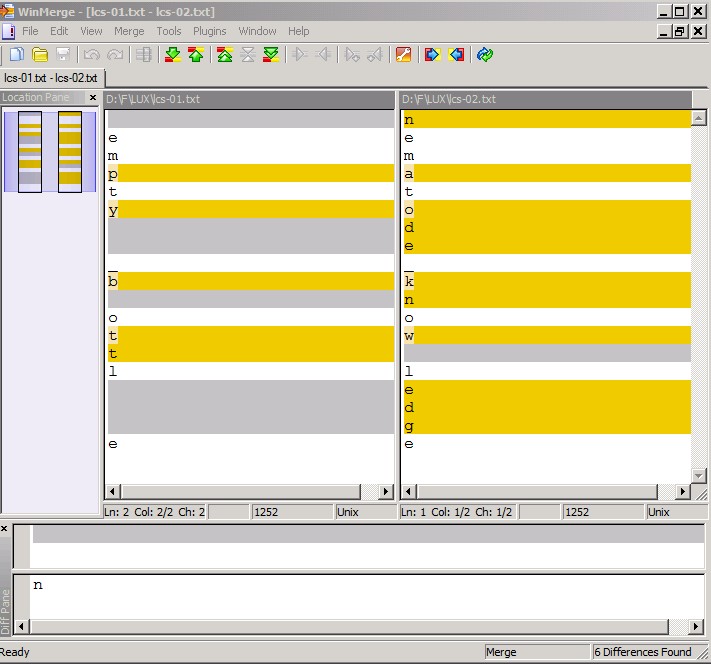
Make each letter a line in a file.
Note: LCS can be used on individual lines to see similarities and differences within a line.
Lines can be made to be similar using regular expression pattern matching.
16. Change management
17. Example in WinMerge
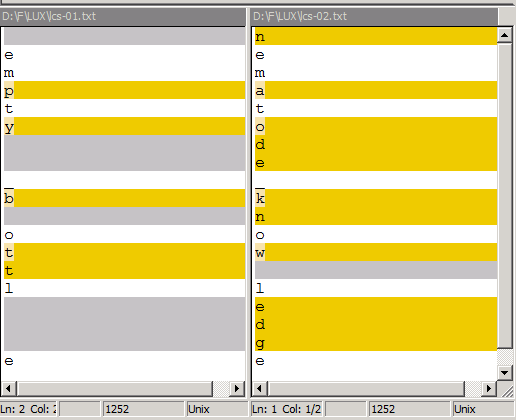
Some analysis/compare programs.
WinMerge
DifMerge
nematode-knowledge
empty-bottle
18. Approach
Approach:
Top down divide and conquer (by 1) for correctness.
Memoization (time efficiency).
Bottom up dynamic programming (time efficiency).
Length only (bootstrap)
Divide and conquer (space efficiency)
Recover solution
19. Program and output
a = "empty_bottle"
b = "nematode_knowledge"
print("a=[" .. a .. "]")
print("b=[" .. b .. "]")
local c = top_down_lcs1(a, b)
print(" c=[" .. c .. "]")
20. Output:
a=[empty_bottle]
b=[nematode_knowledge]
c=[emt_ole]
Time and space efficiency depends on the algorithm used.
21. Possible matches
(a == "nematode-knowledge") and (m == 18)
(b == "empty-bottle") and (n == 12)
possible non-empty substring compares: m*n == 216
22. Start
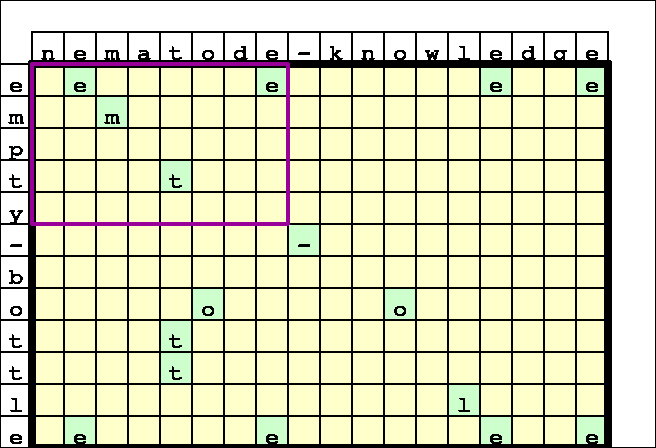
Start from the end of both strings.
23. Compare
Compare both versions for symmetry:
Flip the order of the strings.
Forward or backward in strings.
String or reverse string.
2*2*2 = 8 approaches. All yield the same LCS.
24. Match
25. Non-Match (1)
26. Non-Match (2)
27. Next
28. Recursive top down backward
a 1 a 2 ... a m-1 a m
b 1 b 2 ... b n-1 x n
function lcs_1b(a, b)
local m = #a
local n = #b
if (m == 0) or (n == 0) then
return ""
elseif string.sub(a, m, m) == string.sub(b, n, n) then
return lcs_1b(string.sub(a, 1, m-1), string.sub(b, 1, n-1)) .. string.sub(a, m, m)
else
local a1 = lcs_1b(a, string.sub(b, 1, n-1))
local b1 = lcs_1b(string.sub(a, 1, m-1), b)
return math.max(#a1, #b1)
end
end
Time and space INEFFICIENT!!!
29. Recursive top down forward
a 1 a 2 ... a m-1 a m
b 1 b 2 ... b n-1 x n
function lcs_1f(a, b)
local m = #a
local n = #b
if (m == 0) or (n == 0) then
return ""
elseif string.sub(a, 1, 1) == string.sub(b, 1, 1) then
return string.sub(a, 1, 1) .. lcs_1f(string.sub(a, 2, m), string.sub(b, 2, n))
else
local a1 = lcs_1f(a, string.sub(b, 2, n))
local b1 = lcs_1f(string.sub(a, 2, m), b)
return math.max(#a1, #b1)
end
end
Time and space INEFFICIENT!!!
30. Maximum subsequence length
String rewriting involves copies and is inefficient.
Modify the algorithm to return the length of the maximal subsequence.
Improve the algorithm.
Extract the LCS from the results.
function lcs_2b(a, b)
local m = #a
local n = #b
if (m == 0) or (n == 0) then
return 0
elseif string.sub(a, m, m) == string.sub(b, n, n) then
return lcs_2b(string.sub(a, 1, m-1), string.sub(b, 1, n-1)) + 1
else
local a1 = lcs_2b(a, string.sub(b, 1, n-1))
local b1 = lcs_2b(string.sub(a, 1, m-1), b)
return math.max(a1, b1)
end
end
31. Output
a=[empty_bottle]
b=[nematode_knowledge]
c=[7]
32. Next step
Use a list to store the string symbols.
Pass the ending location.
33. Use a list for A and B
Use a list for A and B.
A = {}
setDefault(A, "")
for i=1,string.len(a) do
A[i] = string.sub(a, i, i)
end
B = {}
setDefault(B, "")
for j=1,string.len(b) do
B[j] = string.sub(b, j, j)
end
io.write("A=[")
for i,a in pairs(A) do
io.write(a)
end
print("]")
io.write("B=[")
for j,b in pairs(B) do
io.write(b)
end
print("]")
34. Modified code
function lcs_3b(A, i, B, j)
if (i == 0) or (j == 0) then
return 0
elseif A[i] == B[j] then
return lcs_3b(A, i-1, B, j-1) + 1
else
local a1 = lcs_3b(A, i, B, j-1)
local b1 = lcs_3b(A, i-1, B, j)
return math.max(a1, b1)
end
end
35. Call
c = lcs_3b(A, #A, B, #B)
print("c=[" .. c .. "]")
36. Observation
Observation: L(i, j) is a maximal possible length common subsequence of A
1i and B
1j.
Initialization of L, the Length matrix.
L = {}
for i=1,#A do
L[i] = {}
for j=1,#B do
L[i][j] = -1
end
end
For convenience, L is initially defined as -1 everywhere (explicitly or via default metatable method).
37. Initial L matrix
L= n e m a t o d e _ k n o w l e d g e
e -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
m -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
p -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
t -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
y -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
_ -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
b -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
o -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
t -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
t -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
l -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
e -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
38. Initial L matrix
39. Compute the L matrix
function lcs_4b(A, i, B, j, L)
local p
if (i == 0) or (j == 0) then
p = 0
else
if A[i] == B[j] then
p = lcs_4b(A, i-1, B, j-1, L) + 1
else
local a1 = lcs_4b(A, i, B, j-1, L)
local b1 = lcs_4b(A, i-1, B, j, L)
p = math.max(a1, b1)
end
L[i][j] = p
end
return p
end
The L matrix is computed.
40. Computed L matrix
L= n e m a t o d e _ k n o w l e d g e
e 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 -1
m 0 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 -1
p 0 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 -1
t 0 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 -1
y 0 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 -1
_ 0 1 2 2 3 3 3 3 4 4 4 4 4 4 4 4 4 -1
b 0 1 2 2 3 3 3 3 4 4 4 4 4 4 4 4 4 -1
o 0 1 2 2 -1 4 4 4 4 4 4 5 5 5 5 5 5 -1
t 0 1 2 2 3 4 4 4 4 4 4 5 5 5 5 5 5 -1
t -1 -1 -1 -1 3 4 4 4 4 4 4 5 5 5 5 5 5 -1
l -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 6 6 6 6 -1
e -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 7
41. Computed L matrix
42. Recover the LCS: approach
43. Recover the LCS: code
To recover the LCS from L, backtrack through the matrix.
function path_extract1(L, A, i, B, j)
if (i == 0) or (j == 0) then
return ""
elseif A[i] == B[j] then
return path_extract1(L, A, i-1, B, j-1) .. A[i]
else
local x1, x2
if j == 1 then
x1 = -1
else
x1 = L[i][j-1]
end
if i == 1 then
x2 = -1
else
x2 = L[i-1][j]
end
if x1 > x2 then
return path_extract1(L, A, i, B, j-1)
else
return path_extract1(L, A, i-1, B, j)
end
end
end
44. Call the extraction
Call as follows.
p = lcs_6b(A, 1, #A, B, 1, #B, L)
print("p=[" .. p .. "]")
c = path_extract1(L, A, #A, B, #B)
print("c=[" .. c .. "]")
This is time efficient but space inefficient!
45. Efficiency
The recursive solution is very inefficient.
Solution: Memoization.
function lcs_5b(A, i, B, j, L)
local p
if (i == 0) or (j == 0) then
p = 0
else
p = L[i][j]
if p < 0 then
if A[i] == B[j] then
p = lcs_5b(A, i-1, B, j-1, L) + 1
else
local a1 = lcs_5b(A, i, B, j-1, L)
local b1 = lcs_5b(A, i-1, B, j, L)
p = math.max(a1, b1)
end
L[i][j] = p
end
end
return p
end
The same L matrix is computed.
46. Add the start and stop indexes
function lcs_6b(A, i1, i2, B, j1, j2, L)
local p2
if (i2 < i1) or (j2 < j1) then
p = 0
else
p = L[i2][j2]
if p < 0 then
if A[i2] == B[j2] then
p = lcs_6b(A, i1, i2-1, B, j1, j2-1, L) + 1
else
local a1 = lcs_6b(A, i1, i2, B, j1, j2-1, L)
local b1 = lcs_6b(A, i1, i2-1, B, j1, j2, L)
p = math.max(a1, b1)
end
L[i2][j2] = p
end
end
return p
end
The same L matrix is computed.
Note: Recursion can be converted to iteration. Left as an exercise.
47. Source

Accessible 3-page paper with which to get started.
48. Source

(page 2/3)
49. Source

(page 3/3)
50. Source
A linear space algorithm for computing maximal common subsequences
D. S. Hirschberg, Princeton University
1975.
51. Hirschberg Approach
52. Hirschberg Approach
53. Hirschberg Approach
54. Hirschberg Approach
55. Hirschberg Approach
56. Animation
57. Hirschberg (full L, rows)
function dpa_traverse_4(L, A, B, i1, i3, j1, j3, dx)
for i=i1,i3,dx do
for j=j1,j3,dx do
if A[i] == B[j] then
if (i == i1) or (j == j1) then
L[i][j] = 1
else
L[i][j] = 1 + L[i-dx][j-dx]
end
else
local y1, y2
if i == i1 then
y1 = 0
else
y1 = L[i-dx][j]
end
if j == j1 then
y2 = 0
else
y2 = L[i][j-dx]
end
L[i][j] = math.max(y1, y2)
end
end
end
end
58. Hirschberg (full L, main)
function lcs_hirschberg_4(L, A, B, i1, i3, j1, j3, level)
if not L[level] then
L[level] = initL1(A, B)
hlist1[level] = {}
end
if j1 > j3 then
for i=i1,i3 do
extractPut1(A[i]," ",1)
end
elseif i1 == i3 then
table.insert(hlist1[level], 4 .. " " .. #ts1 - i1+ 1 .. " " .. #ts1 - i3 .. " " .. j1 .. " " .. j3 .. " 1.5 (" .. "990099" .. ") doBox4")
local j2 = 0
for j=j3,j1,-1 do
if (A[i1] == B[j]) and (j2 == 0) then
j2 = j
extractPut1(A[i1],B[j],1)
else
extractPut1(" ",B[j],1)
end
end
if j2 == 0 then
extractPut1(A[i1]," ",1)
else
table.insert(hlist1[level], 5 .. " " .. #ts1 - i1+ 1 .. " " .. #ts1 - i3 .. " " .. j2 .. " " .. j2 .. " 0.5 (" .. "00CC00" .. ") doBox4")
table.insert(hlist1[level], 0 .. " " .. j2 .. " " .. #ts1 - i1 .. " " .. string.byte(A[i1]) .. " " .. "(CCFFCC) putChar2")
end
else
local i2 = math.floor((i1+i3)/2)
dpa_traverse_4(L[level], A, B, i1, i2, j1, j3, 1)
dpa_traverse_4(L[level], A, B, i3, i2+1, j3, j1, -1)
local j2 = j1-1
local k1 = 0
for j=j1,j3 do
local k
k = L[level][i2][j] + L[level][i2+1][j]
if k > k1 then
k1 = k
j2 = j
end
end
table.insert(hlist1[level], 1 .. " " .. #ts1 - i1+ 1 .. " " .. #ts1 - i2 .. " " .. j1 .. " " .. j2 .. " 1.0 (0000CC) doBox4")
table.insert(hlist1[level], 1 .. " " .. #ts1 - i2 .. " " .. #ts1 - i3 .. " " .. j2+1 .. " " .. j3 .. " 1.0 (0000CC) doBox4")
table.insert(hlist1[level], 2 .. " " .. #ts1 - i1+ 1 .. " " .. #ts1 - i3 .. " " .. j1 .. " " .. j3 .. " 1.0 (000000) doBox4")
table.insert(hlist1[level], 3 .. " " .. #ts1 - i2 - 1 .. " " .. #ts1 - i2 + 1 .. " " .. j1 .. " " .. j3 .. " 1.0 (CC0000) doBox4")
lcs_hirschberg_4(L, A, B, i1, i2, j1, j2, level+1)
lcs_hirschberg_4(L, A, B, i2+1, i3, j2+1, j3, level+1)
end
end
59. Change management
60. End of page

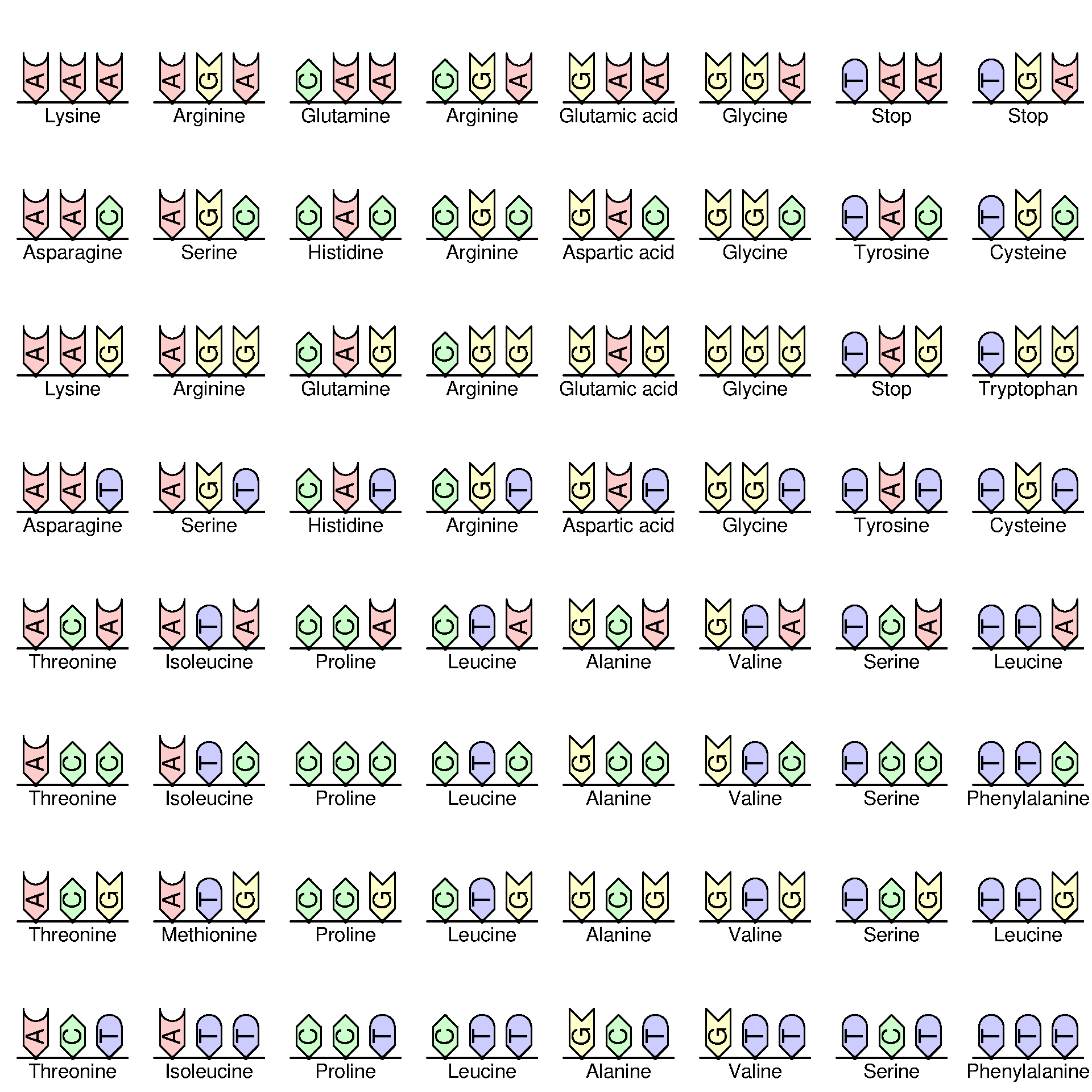 Three nucleotides go together to specify one amino acid (or start or stop instructions).
Three nucleotides go together to specify one amino acid (or start or stop instructions).
 File comparison: (line oriented, useful for regression testing, etc.):
File comparison: (line oriented, useful for regression testing, etc.):
 File comparison: (line oriented, useful for regression testing, etc.):
File comparison: (line oriented, useful for regression testing, etc.):
 Make each letter a line in a file.
Make each letter a line in a file.