Send
Close Add comments:
(status displays here)
Got it! This site "robinsnyder.com" uses cookies. You consent to this by clicking on "Got it!" or by continuing to use this website. Note: This appears on each machine/browser from which this site is accessed.
Truth tables: programmed method
1. Programmed method
A programming language can be easily used to automate the generation of a given truth table.
It helps to understand the manual method for constructing extended truth tables before trying the programmed method. If you are unsure about the manual method, see
Truth tables: manual method .
2. Logical expression
Consider the following (fully parenthesized) logical expression that is given.
( X & Y ) | ( ( ! X ) & ( ! Y ) )
3. Truth table using manual method
Here is the extended truth table for this logical expression.
X Y | ( X & Y ) | ( ( ! X ) & ( ! Y ) )
---------------------------------------
0 0 | ( 0 0 0 ) 1 ( ( 1 0 ) 1 ( 1 0 ) )
0 1 | ( 0 0 1 ) 0 ( ( 1 0 ) 0 ( 0 1 ) )
1 0 | ( 1 0 0 ) 0 ( ( 0 1 ) 0 ( 1 0 ) )
1 1 | ( 1 1 1 ) 1 ( ( 0 1 ) 0 ( 0 1 ) )
Again, if you are unsure about the manual method, see
Truth tables: manual method .
4. Expression tree
Here is an expression tree for the above logical expression.
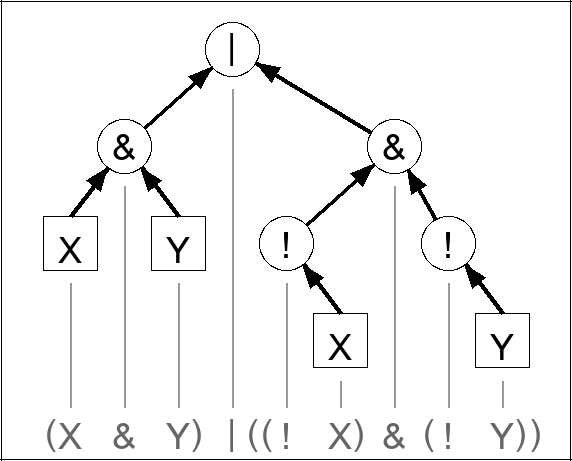
The goal now is to write a program that automates this process for this specific expression.
5. Assign variables
The first step is to give each logical operator in the logical expression a distinct name. Here the variables are named with a single letter starting at
A. Here is the expression.
( X & Y ) | ( ( ! X ) & ( ! Y ) )
Here are the variables needed.
A corresponds to the leftmost "&" (and)
B corresponds to the only "|" (or)
C corresponds to the leftmost "!" (not)
D corresponds to the rightmost "&" (and)
E corresponds to the rightmost "!" (not)
Note that upper case letters are used here, but the actual variables in program code will (usually) be lowercase letters.
6. Correspondence
Here is the expression written using operators and the expression written using variables for comparison.
X Y | ( X & Y ) | (( ! X ) & ( ! Y ))
X Y | ( X A Y ) B (( C X ) D ( E Y ))
7. Expression tree
Here is the expression tree using operators.
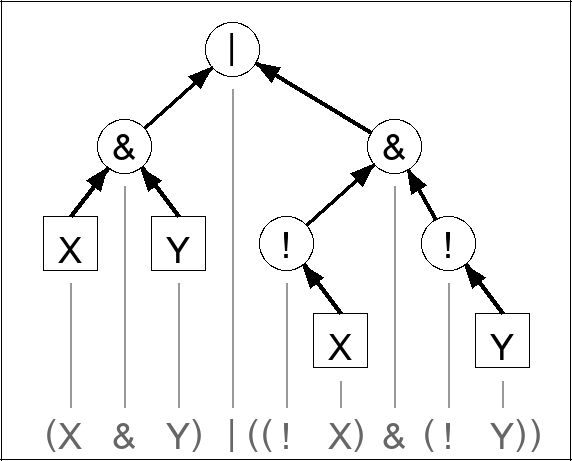
8. Expression tree
Here is the expression tree using variables.
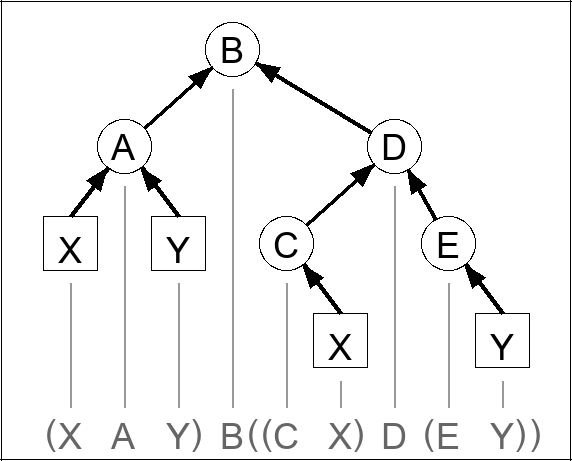
9. Logical operations using integers
We need a way to do logical operations of
x and
y where
x and
y are integers.
negation: ! x is 1 - x
conjunction: x & y is x * y
disjunction: x | y is x + y - x*y
exclusive or: x ^ y is (x + y) % 2
equality: x = y is x + y + 1
To verify the above, check every possible combination. See
Boolean operations using integers .
10. Assignment statements
Assume that the values in variables
x and
y are valid. That is, only
1 or
0. Then a sequence of assignment statements can be used to compute all of the results in the following manner.
a = x * y
c = 1 - x
e = 1 - y
d = c * e
b = a + d - a*d;
Such a sequence of assignments follows the diagram as the data and result flow from leaves at the bottom of the tree to the final result at the top of the tree.
11. Python code and output
Here is the Python code [#1]
Here is the output of the Python code.
12. Walrus operator
Now let us write the same program using the Python walrus operator to assign subexpression values to variables.
13. Python code and output
Here is the Python code [#2]
Here is the output of the Python code.
14. Walrus operator
The walrus operator can make for more compact code. But is it more clear than explicit assignment statements?
15. End of page
